Mathematics of Rendering

Vectors and Matrices

Basic Vector Operations

Vector Magnitude(백터의 크기)

• 백터의 크기를 구하는 공식은 다음과 같다.

\[\|V\| = \sqrt{\sum_{i=0}^{n-1} v_i^2}\]

• 3-Dimensions(3차원 공간)에서 위 공식을 적용해 보면 $|V| = \sqrt{V_x^2 + V_y^2 + V_z^2}$ 으로 된다.
• 벡터의 각각의 성분을 제곱해서 $\sqrt{}$ 연산을 하면 우리는 벡터의 크기를 구할 수 있다.

unit Vector

• unit vector는 크기가 1인 벡터를 의미한다.
• 방향성만 가진 벡터를 구하기 위한 방법이다. 벡터의 크기로 벡터를 나누어 주면 된다.
• 우리는 이것을 Vector를 Normalize 했다고 한다. 공식은 아래와 같다.

\[\hat{V} = \frac{V}{\|V\|}\]

Vector의 덧셈 및 곱셈에 관한 성질

속성	설명
$(a+b) + c = a + (b+c)$	덧셈에 관한 결합법칙
$a+b = b+a$	덧셈 교환법칙
$(st)a = s(ta)$	스칼라 곱에 관한 결합 법칙
$ta = at$	스칼라 곱에 관한 교환 법칙
$t(a+b) = ta +tb$	스칼라 곱에 대한 분배법칙
$(s+t)a = sa +ta$	스칼라 곱에 대한 분배법칙

벡터 끼리의 곱셈에서 교환 법칙은 성립하지 않으며, 스칼라 곱에 대한 교환법칙만 존재 한다.

Matrix(행렬) 의 기초

• A 행력과 B 행렬이 다음과 같다.
  A는 $n \times p$ 행렬 이고 B는 $p\times m$ 인 경우, i 와 j 번째 요소를 구하는 식은 다음과 같다.

\[(AB)_{ij} = \sum_{k=0}^{p-1}A_{ik}B_{kj}\]

Matrix Multiplication Transpose

• 행렬에서 곱셈을 Transpose 하는 공식은 다음과 같다.

\[(AB)_{ij}^T = \sum_{k=0}^{p-1}B_{ik}^{T}A_{kj}^{T}\]

antisymmetic matrix OR skew-symmetric matrix

• 반대칭 혹은 비대칭 행렬이라고 한다.
• 공식은 \(M^{T}_{ij}=-M_{ij}\) 이다.

\[\begin{bmatrix} 0 & 1 & -4 \\[0.5em] -1 & 0 & 7 \\[0.5em] 4 & -7 & 0 \\[0.5em] \end{bmatrix}\]

벡터의 표기법

Column Vector

\[v= (v_0, v_1, \dots, v_{n-1}) = \begin{bmatrix} v_0 \\ v_1 \\ \vdots \\ v_{n-1} \end{bmatrix}\]

Row Vector

\[v^T = \begin{bmatrix} v_0 & v_1 & \dots v_{n-1} \end{bmatrix}\]

Vector Multiplication

Dot Product (내적)

\[a \cdot b = \sum_{i=0}^{n-1}a_ib_i\]

위 공식을 3차원 에서 적용해 보면 아래와 같다.
각 성분끼리 곱해서 더한다.

$a \cdot b = a_xb_x + a_yb_y + a_zb_z$

아래와 같이 표현 하기도 한다.

\[a \cdot b = \begin{bmatrix} a_0 & a_1 & \dotsb & a_{n-1} \end{bmatrix} \begin{bmatrix} b_0 \\[0.2em] b_1 \\[0.2em] \vdots \\[0.2em] b_{n-1} \end{bmatrix}\]

벡터의 기하학적 의미 공식은

\[a \cdot b = \|a\|\|b\|\cos\theta\]

여기서 우리가 알 수 있는 사실은 $\theta$ 가 $90^\circ$인 경우 내적의 값은 0이 되며,
a 벡터와 b벡터가 직교하는 경우 내적의 값은 0이 된다는 것을 알수 있다.

여기서 특별한 케이스인 자기 자신과 dot product는 아래와 같은 특징이 있다.

\[v^2 = V \cdot V = \|V\|^2\]

참고로 $|V|$ 는 아래와 같다.

\[\|V\| = \sqrt{\sum_{i=0}^{n-1}v_i^2}\]

내적의 속성

속성	설명
$a \cdot b = b \cdot a$	교환 법칙
$a \cdot (b+c) = a \cdot b + a \cdot c$	분배 법칙
$(ta)\cdot b = a \cdot (tb) = t(a \cdot b)$	인수분해

Cross Product (외적)

2개의 3차원 Vector에서 다음과 같은 공식

\[a \times b = (a_yb_z - a_zb_y, a_zb_x - a_xb_z, a_xb_y - a_yb_x)\]

외적(Cross Product)는 특수한 3X3 비대칭 행렬을 정의해서 나타낼 수도 있다.

\[[a]_X = \begin{bmatrix} 0 & -a_z & a_y \\ a_z & 0 & -a_x \\ -a_y & a_x & 0 \end{bmatrix}\] \[a \times b = [a]_Xb = \begin{bmatrix} 0 & -a_z & a_y \\ a_z & 0 & -a_x \\ -a_y & a_x & 0 \end{bmatrix} \begin{bmatrix} b_x \\ b_y \\ b_z \end{bmatrix} = \begin{bmatrix} -a_zb_y + a_yb_z \\ a_zb_x - a_xb_z \\ -a_yb_x + a_xb_y \\ \end{bmatrix}\]

외적의 크기 공식

\[\|a \times b\| = \|a\| \|b\|\sin{\theta}\]

또한 외적의 크기는 기하학적 의미로는 평행사변형의 넓이에 해당 한다.

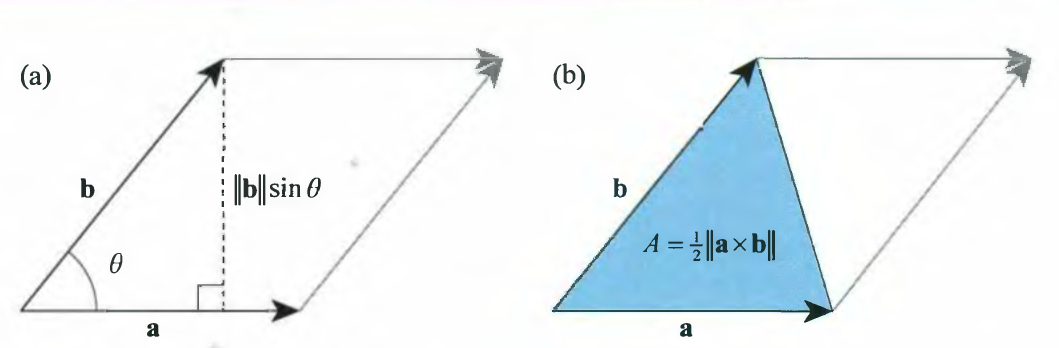
외적은 $a \times b = -b \times a$ 비가환성 특징을 가진다.

외적의 속성

속성	설명
$a \times b = -b \times a$	외적의 비가환성
$a \times (b + c) = a \times b + a \times c$	외적의 분배법칙
$(ta)\times b = a \times (tb) = t(a \times b)$	스칼라 인수분해
$a\times (b\times c) = b(a\cdot c) - c(a\cdot b)$	Vector triple product
$(a\times b)^2 = a^2b^2 - (a\cdot b)^2$	라그랑주 항등식

Scalar Triple Product

순서에 상관없이 동일한 결과를 나타 냅니다.

\[[a,b,c] = (a\times b)\cdot c = (b\times c)\cdot a = (c\times a)\cdot b\]

Scalar Triple Product의 기하학적 의미는 (parallelepiped)평행육면체의 부피와 같습니다.

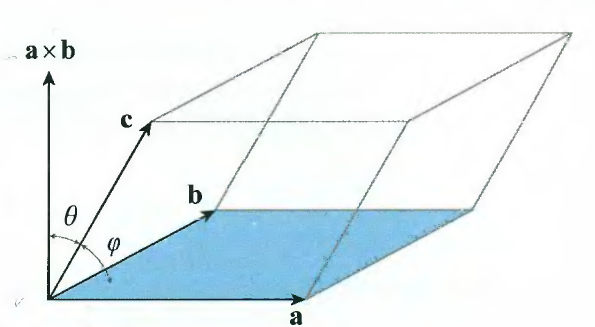
위 그림으로 부터 아래와 같은 공식을 유도할 수 있습니다. ($\theta = 90-\varphi$)

\[(a\times b)\cdot c = \|{a\times b}\|\|c\|\cos\theta = \|a\times b|\|c\|\sin\varphi\]

Vector Projection

x, y, z Axis에 일직선이 되도록 아래의 unit Vector를 정의 한다. i, j ,k 를 아래와 같이 정의 한다.

\[i =(1,0,0) \\[0.3em] j=(0,1,0) \\[0.3em] k=(0,0,1) \\[0.3em]\]

3D Vector를 다음과 같이 표기 할 수 있다.

\[v = v_xi + v_yj + v_zk \\ (v\cdot i = \|v\| \|i\|\cos\theta) \\ \color{red}{i\hspace{0.5em} is\hspace{0.5em} unit\hspace{0.5em}vector} \\ (v_x = v\cdot i,\hspace{0.5em} v_y = v\cdot j,\hspace{0.5em} v_z = v\cdot k) \\ v = (v\cdot i)i + (v\cdot j)j + (v\cdot k)k\]

일반적으로 $\vec{a}$ 를 $\vec{b}$에 Projection(사영) 시킬때 공식은 아래와 같다.

\[a_{\parallel b} = \frac{\vec{a}\cdot \vec{b}}{\|b\|^2}\vec{b}\]

$rejection\hspace{0.5em} \vec{a} \hspace{0.5em} from\hspace{0.5em} \vec{b}$ 의 공식은 다음과 같다.

\[a_{\perp b} = \vec{a} - a_{\parallel b} = \vec{a} - \frac{\vec{a}\cdot \vec{b}}{\|b\|^2}\vec{b}\]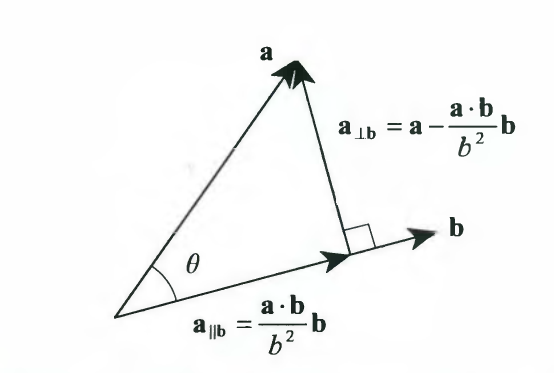

위 그림을 보면 $\hspace{0.5em}\vec{a}\hspace{0.5em} 와\hspace{0.5em} \vec{b}$의 Projection과 Rejection이
직각삼각형의 밑변과 높이에 해당하는 것을 볼 수 있으며, 삼각함수에 따라서 아래와 같은 공식이 된다.

\[\|a_{\parallel b}\| = \|a\|\cos\theta \\ \|a_{\perp b}\| = \|a\|\sin\theta\]

Gram-Schmidt process

Gram-Schmidt process 특정 벡터의 정규직교기저를 구하는 방법이다.
공식은 아래와 같다.

\[\vec{U}_i = \vec{V_i} - \sum_{k=1}^{i-1}(\vec{V_i})_{\parallel \vec{U_k}} = \vec{V_i} - \sum_{k=1}^{i-1}\frac{\vec{V_i}\cdot \vec{U_k}}{\vec{U_k^2}}\vec{U_k}\]

Matrix Inversion

우리는 종종 A좌표계 에서 B좌표계로 변환하는 일을 수행하게 됩니다.
이떄 A -> B로 혹은 B -> A로 좌표계를 변환하게 되는데 이때 우리는 변환 행렬인
$M \hspace{0.5em}, M^{-1}$ 을 찾아야 하며, $M^{-1}$ 을 Inverse Matrix라고 합니다.

Identity Matrices (단위행렬)

Matrix의 곱에 대한 항등원 이라고 생각하면 됩니다.
항등원이란 : 어떤수에 연산을 했을때 자기자신이 나오게 만드는 값

$I$ 는 다음과 같이 정의 됩니다.

\[I_n = \begin{bmatrix} 1&0&\dotsb&0 \\[0.3em] 0&1&\dotsb&0 \\[0.3em] \vdots&\vdots&\ddots&\vdots \\[0.3em] 0&0&\dotsb&1 \\[0.3em] \end{bmatrix} \\[1em] AI_n = A \\ I_nB = B \\[1em] \therefore (IB)_{ij} = \sum_{k=0}^{n-1}I_{ik}B_{kj} = B_{ij}\]

Inverse Matrix(역행렬)의 특징

• n by n 정방행렬(정사각행렬) 에서만 존재 합니다.
• $MM^{-1} = I_n$ 또는 $M^{-1}M = I$ 입니다.
• 역행렬은 항상 존재하지는 않습니다.
• Determinant(행렬식)을 이용해서 존재 유무를 알 수 있습니다.

Determinants (행렬식)

행렬식의 공식은 다음과 같습니다.

\[det(M) = \sum_{j=0}^{n-1}M_{kj}(-1)^{k+j}|M_{\bar{kj}}| \\[0.5em] det(M) = \sum_{i=0}^{n-1}M_{ik}(-1)^{i+k}|M_{\bar{ik}}| \\[0.5em] \because det(M^T) = det(M)\\[0.5em] (|M_{\bar{kj}}|:k행\hspace{0.5em}과\hspace{0.5em}j열을\hspace{0.5em}제외한\hspace{0.5em}Minor\hspace{0.5em}Matrix에\hspace{0.5em}대한\hspace{0.5em} 행렬식)\]

위 공식의 의미는 다음과 같다.

Determinent Property

속성	설명
$det(I_n) = 1$	단위행렬의 행렬식
$det(A^T) = det(A)$	전치행렬의 행렬식
$det(A^{-1}) = 1/det(A)$	역행렬의 행렬식
$det(AB) = det(A)det(b)$	행렬식의 곱 법칙
$det(tA) = t^ndet(A)$	Scalar factorization 의 행렬식

Elementary Matrices (기본행렬)

단위행렬 $I_n$에서 기본행연산(elementary row operation)을 한 번 실행하여 얻어지는 행렬이다.

아래에 3가지의 기본행연산이 있습니다.
(a) 0이 아닌 스칼라 값을 M의 행에 곱합니다.
(b) M의 행의 위치를 바뀌어 줍니다.
(C) 스칼라 값을 곱한 행을 다른행에 더합니다.

기본행 연산 중 (b)의 경우는 행교환을 하게 되면 교환하기 전/후 Matrix Determinant의
부호가 반대가 된다는 사실입니다.

\[\begin{bmatrix} c & d \\ a & b \\ \end{bmatrix} = cb-da = -(ad - bc) = \begin{bmatrix} a & b \\ c & d \\ \end{bmatrix}\]

위 사실을 기반으로 가장 중요한 사실은 동일한 Row를 포함하고 있는 행렬의 행렬식의 값은 0 이라는 사실입니다.
행 교환을 했지만 Matrix자체에 변화가 없기 때문에 유추해 보면 양수와 음수 값이 같은 경우는 0이기 때문입니다.

\[\begin{bmatrix} 1 & 2 \\ 1 & 2 \\ \end{bmatrix} = ad - bc = (1\times2) - (2\times1) = 0\]

Inverse Calculation (역행렬)

• 역행렬을 구한는 방법 두가지를 설명 하고자 합니다.
• Gauss-Jordan Elimination
• Determinant & Cofactor Matrix

Gauss-Jordan Elimination Case

• 기본행 연산의 곱으로 역행렬을 구할 수 있습니다.

\[E_mE_{m-1}\cdots\ E_2E_1M = I\]

• 예제
• 기본행 연산을 양쪽 행렬에 동일하게 적용한다.

\[\left[ \begin{array}{ccc|ccc} 1&0&1& 1&0&0 \\ 0&2&1& 0&1&0 \\ 1&1&1& 0&0&1 \\ \end{array} \right] \\[2em] \left[ \begin{array}{ccc|ccc} 1&0&1& 1&0&0 \\ 0&2&1& 0&1&0 \\ 0&1&0& -1&0&1 \\ \end{array} \right] row1\times(-1) + row3 \\[2em] \left[ \begin{array}{ccc|ccc} 1&0&1& 1&0&0 \\ 0&1&0& -1&0&1 \\ 0&2&1& 0&1&0 \\ \end{array} \right] row2\hspace{0.3em}와\hspace{0.3em}row3\hspace{0.3em}행교환 \\[2em] \left[ \begin{array}{ccc|ccc} 1&0&1& 1&0&0 \\ 0&1&0& -1&0&1 \\ 0&0&1& 2&1&-2 \\ \end{array} \right] row2\hspace{0.3em}\times(-2)+row3 \\[2em] \left[ \begin{array}{ccc|ccc} 1&0&0& -1&-1&2 \\ 0&1&0& -1&0&1 \\ 0&0&1& 2&1&-2 \\ \end{array} \right] row3\hspace{0.3em}\times(-1)+row1 \\[3em] \therefore M^{-1} = \begin{bmatrix} -1&-1&2 \\[0.3em] -1&0&1 \\[0.3em] 2&1&-2 \\[0.3em] \end{bmatrix} \\\]

Determinant & Cofactor Matrix Case

\[(Cofactor)\hspace{0.3em} C_{ij} = (-1)^{i+j}|M_{\bar{ij}}| \\[0.5em] (adjugate\hspace{0.3em}of\hspace{0.3em}the\hspace{0.3em}matrix\hspace{0.3em}M) = C^T(M)\\[0.5em] \therefore M^{-1} = \frac{C^T(M)}{det(M)}\]

• $3\times3$ 행렬의 경우는 다음과 같이 벡터로 계산 할 수 있음.

\[(M =\begin{bmatrix} \vec{a} & \vec{b} & \vec{c} \end{bmatrix}) \\[0.8em] M^{-1} = \frac{1}{[\vec{a},\vec{b},\vec{c}]} \begin{bmatrix} \vec{b}\times \vec{c} \\ \vec{c}\times \vec{a} \\ \vec{a}\times \vec{b} \\ \end{bmatrix}\]

$4 \times 4$ Matrix에서 $M^{-1}$을 구하는 효율적인 방법.

• 처음 3개 행에 대한 Column Vector $\vec{a},\vec{b},\vec{c},\vec{d}$ 와 4번째(마지막)행인 x, y, z, w를 다음과 같이 설정.

\[M = \begin{bmatrix} \uparrow & \uparrow & \uparrow & \uparrow & \\ a & b & c& d \\ \downarrow & \downarrow & \downarrow & \downarrow & \\ \hdashline x & y & z & w \end{bmatrix}\]

• 그 다음 우리는 $\vec{s},\vec{t},\vec{u},\vec{v}$를 다음과 같이 정의 합니다.

\[\vec{s} = \vec{a}\times \vec{b} \\ \vec{t} = \vec{c}\times \vec{d} \\ \vec{u} = y\vec{a} - x\vec{b} \\ \vec{v} = w\vec{c} - z\vec{d} \\[1em] \therefore det(M) = \vec{s}\cdot \vec{v} + \vec{t} \cdot \vec{u} \\[0.5em] \therefore M^{-1} = \frac{1}{\vec{s}\cdot \vec{v} + \vec{t} \cdot \vec{u}} \left[ \begin{array}{c:c} \vec{b}\times \vec{v}+y\vec{t} & -\vec{b}\cdot\vec{t} \\ \vec{v}\times\vec{a} - x\vec{t} & \vec{a}\cdot{t} \\ \vec{d}\times\vec{u} + w\vec{s} & -\vec{d}\cdot{\vec{s}} \\ \vec{u}\times\vec{c} - z\vec{s} & \vec{c}\cdot{\vec{s}} \end{array} \right]\]

• 역행렬$M^{-1}$의 처음 3개의 컬럼은 위 4개의 3차원 행 벡터 에 의해서 채워 짐
• 역행렬$M^{-1}$의 4번째 컬럼은 4차원 벡터 $(-\vec{b}\cdot\vec{t},\vec{a}\cdot{t},-\vec{d}\cdot{\vec{s}},\vec{c}\cdot{\vec{s}})$ 에 의해서 채워 짐
• 대부분 게임엔진에서 $M$ 행렬의 4번재 Row는 $\begin{bmatrix} 0&0&0&1 \end{bmatrix}$ 이므로
• $x=y=z=0,\hspace{0.3em} w=1$ 이고, $\vec{u}=0, \vec{v}=\vec{c}$ 이 된다.

Transforms

Coordinate Spaces

Transformation Matrices

Position $p_A$ A의 좌표계로 부터 Position $p_B$ B 좌표계로 변환하는 표현은 아래와 같다.

\[p_B = Mp_A + \vec{t}\\ (affine\hspace{0.5em} transformation) \\\]

• $M$ 은 $3\times3$ Matrix, $\vec{t}$는 3D Translation Vector 이며 좌표계의 Origin(원점)을 이동시킵니다.
• 우리는 역으로 B의 좌표계에서 A의 좌표계로 변환 할 수도 있습니다.

\[p_a = M^{-1}(p_b - \vec{t})\]

• $M$과 $\vec{t}$는 $4\times4$ matrix로 표현 할 수 있습니다. 그 전까지는 일단 $\vec{t}$는 무시하고

• 원점(origin)은 같다는 전제하에 $3\times3$ 매트릭스 에만 당분간 집중 합니다.

• 일반적인 Linear trasnformation(원점이 동일한)은 아래와 같이 나타 냅니다.

\[v_b = Mv_a \\[0.5em] M=\begin{bmatrix} a & b & c \end{bmatrix} \\[0.5em] Then \\ M\begin{bmatrix} 1\\ 0\\ 0\\ \end{bmatrix} = a, \hspace{0.5em} M\begin{bmatrix} 0\\ 1\\ 0\\ \end{bmatrix} = b, \hspace{0.5em} M\begin{bmatrix} 0\\ 0\\ 1\\ \end{bmatrix} = c \hspace{0.5em} \\[0.8em] \therefore Mv = v_xa + v_yb + v_zc\]

Orthogonal Transformation (직교변환)

• 게임 엔진에서 대부분 Transform Matrices를 Perpendicular unit-length columns(직교 유닛 컬럼)으로 표헌합니다.
• 이러한 Matrices를 우리는 Orthogonal matrices(직교 행렬) 이라고 합니다.
• 아래는 모두 같은 의미를 지닙니다.
  1. M은 Orthogonal Matrix(직교행렬) 이다.
  2. $M^{-1} = M^T$는 같다.
  3. $M$은 columns Mutually Perpendicular unit-length
  4. $M$은 rows Mutually Perpendicular unit-length

Transform Composition

• Transform $A$ 는 A좌표계 에서 적용된 변환이라고 한다면, 그와 동등한 B좌표계에서의 변환은 아래와 같습니다.
• 행렬 $M$ 은 좌표계 $A \rightarrow B$ 로 변환행렬.
• 행렬 $M^{-1}$ 은 좌표게 $B \rightarrow A$로 변환행렬.

\[B=MAM^{-1}\]

Rotations (회전)

• 어떤 $\vec{v}$를 z축을 기준으로 회전 시키려고 합니다.
• $\vec{v}$를 다음과 같이 표기 합니다.
• $\vec{v} = v_xi + v_yj + v_zk$
• i,j,k는 좌표축과 평행한 unit vector입니다.
• $k$는 z axis와 평행하므로 변화가 없고, $v_xi + v_yj$만 변화될 것입니다.

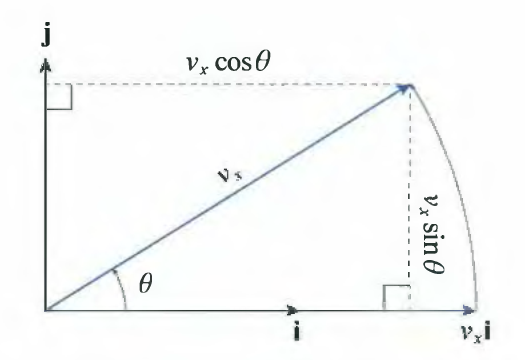
• 위 그림에서 $v_x\vec{i}$를 $\theta$ 만큼 회전 시키면 아래와 같습니다.
• $\vec{i}$는 $unit\hspace{0.5em} vector$ 입니다.

\[v_x\cos\theta\vec{i} + v_x\sin\theta\vec{j}\]

• 또 한 우리는 $v_y\vec{j}$도 계산해 줘야 합니다.
• 위 그림의 j축을 기준으로 $\theta$ 만큼 회전한 값을 구해주면 아래와 같습니다.

\[v_y\cos\theta\vec{j} - v_y\sin\theta\vec{i}\] \[\vec{v}' = (v_x\cos\theta - v_y\sin\theta)\vec{i} + (v_x\sin\theta + v_y\cos\theta)\vec{j} + v_z\vec{k} \\[1em] \therefore \begin{bmatrix} v'_x \\[0.3em] v'_y \\[0.3em] v'_z \\[0.3em] \end{bmatrix} = \begin{bmatrix} \cos\theta & -\sin\theta & 0 \\[0.3em] \sin\theta & \cos\theta & 0 \\[0.3em] 0 & 0 & 1 \\[0.3em] \end{bmatrix} \begin{bmatrix} v_x \\[0.3em] v_y \\[0.3em] v_z \\[0.3em] \end{bmatrix}\]

• 최종적으로 X, Y, Z 축에 대한 공식은 아래와 같습니다.

Rotation about an Arbitrary Axis (임의의 축에 대한 회전)

• 하지만 일반적으로 회전을 할 때, 임의의 축을 중심으로 회전 할 경우가 더 많다.

\[\|v\|\sin\alpha = v_{\perp a} = a\times v \hspace{0.5em}(same\hspace{0.5em}length.)\\ \\ \therefore v' = v_{\parallel{a}} + v_{\perp{a}}\cos\theta + (a\times v)\sin\theta\]

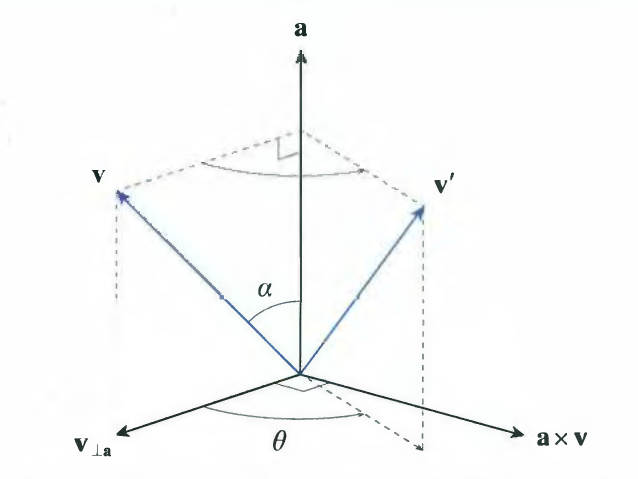
• projection과 rejection의 정의에 의해서 아래와 같이 정의된다.
• $\vec{a} = unit\hspace{0.5em}vector$ 이기 때문에 $a^2$은 생략한다.(Projection 공식에서)
• $a , v$ 는 벡터 입니다.

\[v' = (v\cdot{a})a + [v-(v\cdot{a})a]\cos\theta + (a\times{v})\sin\theta \\[0.5em] v' = v\cos\theta + (v\cdot a)a(1-\cos\theta) + (a\times v)\sin\theta \\[0.5em] \because (v\cdot a)a = (a\otimes a)v \hspace{0.3em} 이므로 \\[0.5em]\]

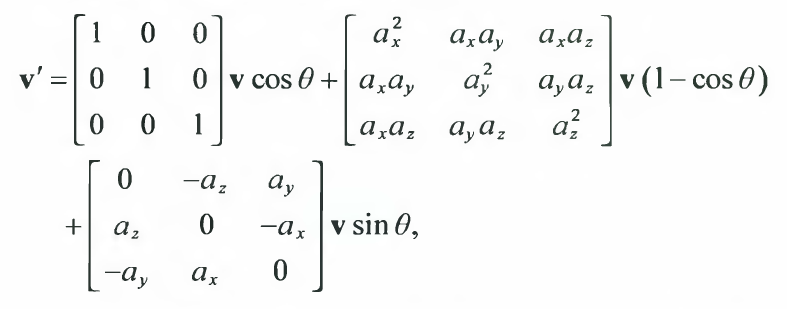
• $c=\cos\theta$, $s=\sin\theta$

Reflections (반사)

• 게임엔진에서 거울이나 물표면에 반사되는 변환을 나타낼때 많이 사용 된다.

\[\vec{v} = \vec{v}_{\perp{a}}+\vec{v}_{\parallel a}\\[0.3em] \vec{v'} = \vec{v}_{\perp a} - \vec{v}_{\parallel a}\]

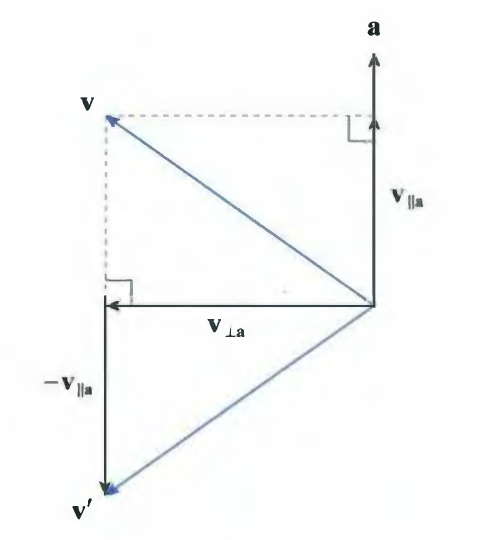
Scales

• 객체의 사이즈를 확장 하거나 축소하는 변환 입니다.
• Uniform Scale : 모든 방향이 동일한 크기로 확장 하는것.
• Nonuniform Scale : 어떤 한 방향이 다른 방향에 비해서 크거나 작은 크기로 확장 되는것.

\[M_{scale}(s_x, s_y, s_z) = \begin{bmatrix} s_x & 0 & 0 \\[0.3em] 0 & s_y & 0 \\[0.3em] 0 & 0 & s_z \\[0.3em] \end{bmatrix}\]

• 우리는 x, y, z 축 이 아닌 특정 방향 $\vec{a}$ 대해서 확대/축소 할 수도 있습니다.

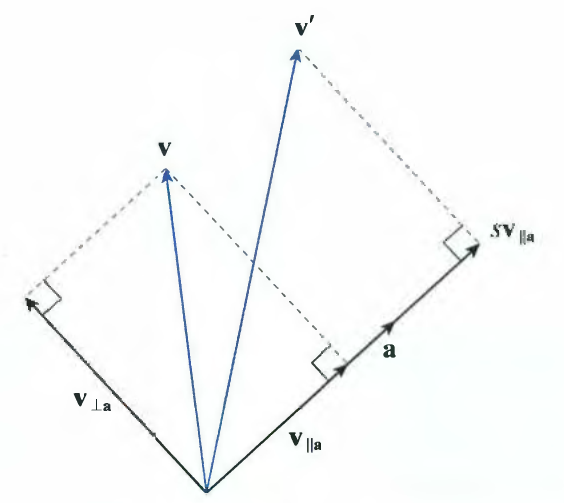
• 위 그림으로 아래와 같은 공식을 유도 할 수 있습니다.

\(\vec{v'} = s\vec{v_{\parallel a}} + \vec{v_{\perp a}} \\[0.5em] = s(\frac{v\cdot a}{\|a\|^2}a) + (v-\frac{v\cdot a}{\|a\|^2}a) \\[0.3em] = s(v\cdot a)a + v-(v\cdot a)a \\[0.3em] = (s-1)(v\cdot a)a - v \\[0.3em] = (s-1)(a\otimes a)v - v \\[0.3em] = (s-1) \begin{bmatrix} a_x \\ a_y \\ a_z \\ \end{bmatrix} \begin{bmatrix} a_x & a_y & a_z \end{bmatrix} - \begin{bmatrix} 1&0&0 \\ 0&1&0 \\ 0&0&1 \\ \end{bmatrix}v\)

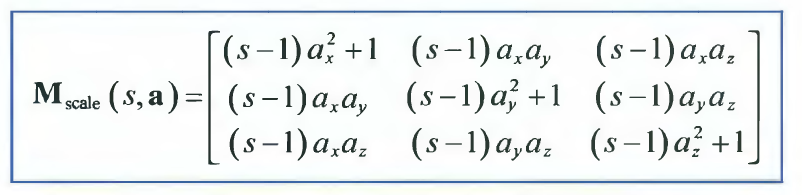
Skews

• Skews를 그림으로 설명하면 다음과 같습니다.

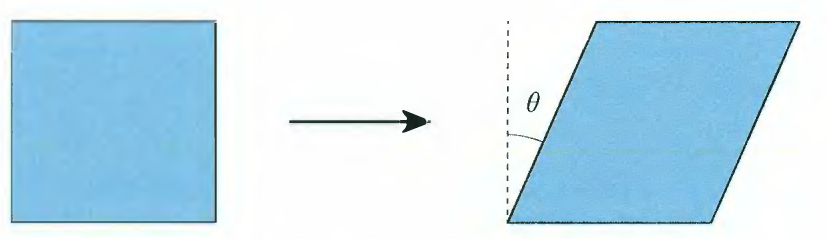
• 공식은 아래와 같이 유도 된다.
• $v’ = v + a(b\cdot v)\tan\theta$
  

\[v' = v + a(b\cdot v)\tan\theta \\ = Iv + (a\otimes b)v\tan\theta \\ = (I + (a\otimes b)\tan\theta)v\]

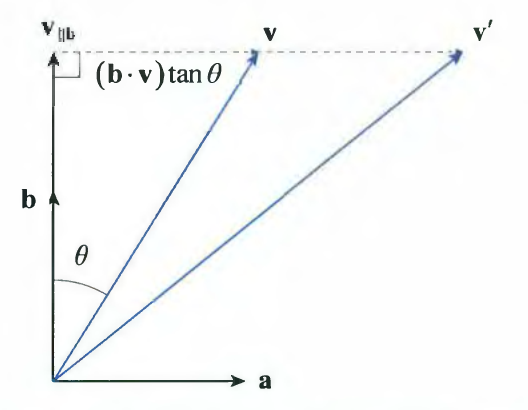
• 만약 a 와 b가 좌표시스템의 축과 같다면, $a = (1,0,0)$ , $b = (0,1,0)$
• 공식은 아래와 같이 더 간결해 집니다.

\[M_{skew}(\theta, i, j) = \begin{bmatrix} 1 & \tan\theta & 0 \\[0.3em] 0& 1 & 0 \\[0.3em] 0& 0 & 1 \\[0.3em] \end{bmatrix}\]

Homogeneous Coordinates (동차 좌표)

• 일반 적인 Affine Transformation 좌표계A 에서 좌표계 B로 의 공식

\[p_b = Mp + t\]

• $4\times4$ 매트릭스로 나타내면 다음과 같다.

\[H = \begin{bmatrix} M & t \\ 0 & 1 \\ \end{bmatrix} = \left[ \begin{array}{ccc|c} M_{00} & M_{01} & M_{02} & t_x \\[0.3em] M_{10} & M_{11} & M_{12} & t_x \\[0.3em] M_{20} & M_{21} & M_{22} & t_x \\[0.3em] \hdashline 0 & 0 & 0 & 1 \\[0.3em] \end{array} \right]\]

Quaternions

Quaternion Fundamentals

• x, y, z, and w are real number
• three imaginary units $i$,$y$, and $k$
  \(q = xi + yj + zk + w\)

\[i^2 = j^2 = k^2 = ijk = -1 \\ ij = -ji = k \\ jk = ikj = i \\ ki = -ik = j \\\]

• 두개의 Quaternions를 곱하면 다음과 같이 계산 됩니다.
  

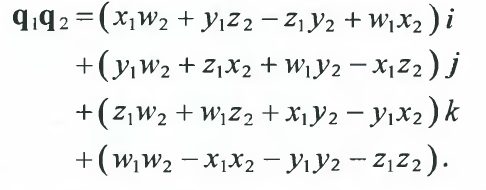
• $q1 = v_1 + s_1$ 이고 $q_2 = v_2+s_2$ 이므로
  \(q_1q_2 = v_1\times{v_2} + s_1v_2 + s_2v_1 + s_1s_2 - v_1\cdot{v_2} \\ q_2q_1 = q_1q_2 - 2(v_1\times{v_2})\)

• $q$의 켤레수는 $q^*$로 표현 한다. \(q = v+s \\ q^* = -v+s \\ qq^* = q^*q = v^2 + s^2\)

• quaternion의 magnitude는 아래와 같다.
  \(\boxed{\|q\| = \sqrt{qq^*} = \sqrt{v^2 + s^2}} \\\) \(\|q_1q_2\| = \|q_1\|\|q_2\|\)

• multiplicative inverse
  \(\boxed{q^{-1} = \frac{q^*}{qq^*} = \frac{-v+s}{v^2 + s^2}}\)

• quaternions의 성질
  

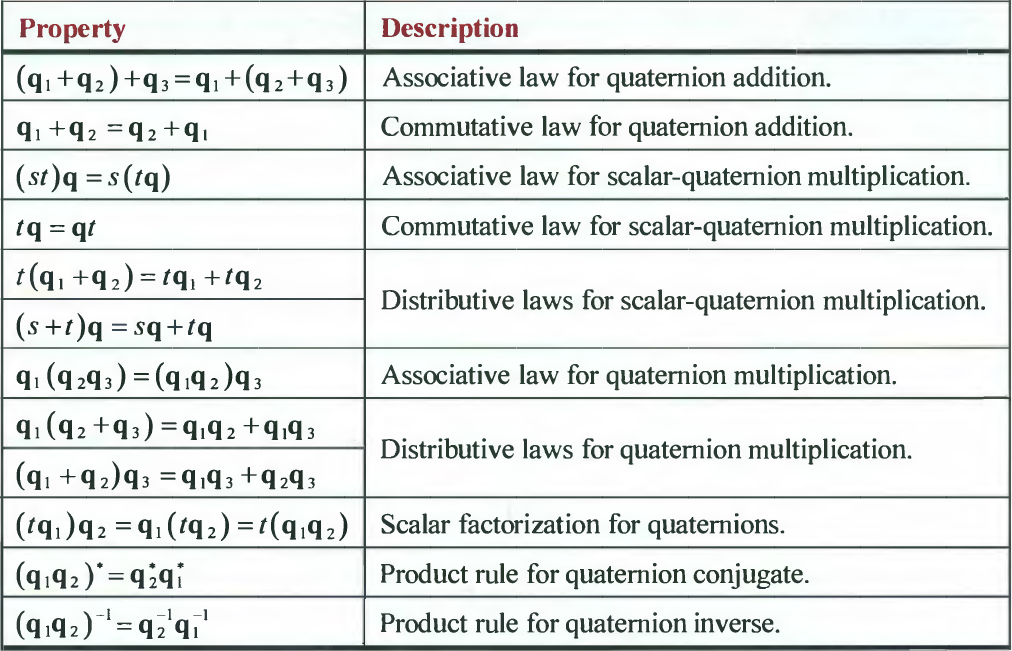
Rotations With Quaternions

• $q = xi + yj + zk + w$ 그리고, $v = (v_x, v_y, v_z)$ 이고

• 최종적으로 $v$에 의해서 회전된 $v’$은 다음과 같다. \(v' = qvq^{-1}.\)

• $q$가 unit quaternion 일 경우 \(\boxed{v' = qvq^*}\)

• $q = b + c$ 라고 하면, $qv$ 는 $qv = (b+c)v = b\times v + cv - b\cdot v$
• 또 $q^* = -b+c$ 입니다.

• $qvq^*$는 아래와 같습니다. \(qvq^* = (b\times v + cv - b\cdot v)(-b + c) \\ = (c^2 - b^2)v + 2(v\cdot b)b + 2c(b\times v)\)

• $-b\times v\times b = (b\cdot v) -b^2v$ 라면

\[qvq^* = (c^2 - s^2)v + 2s^2(v\cdot a)a + 2cs(a\times v) \\[1em] c^2 - s^2 = \cos\theta \\ 2s^2 = 1-\cos\theta\\ 2cs = \sin\theta. \\[1em] c = \cos\frac{\theta}{2} \\[0.5em] s = \sin\frac{\theta}{2}\] \[\boxed{q = (\sin\frac{\theta}{2})a + \cos\frac{\theta}{2}}\]